Homogenous coordinates explain as projector on the screen

https://www.tomdalling.com/blog/modern-opengl/explaining-homogenous-coordinates-and-projective-geometry/

In this article I'm going to explain homogeneous coordinates (a.k.a. 4D coordinates) as simply as I can. In previous articles, we've used 4D vectors for matrix multiplication, but I've never really defined what the fourth dimension actually is. Now it's time to take a closer look at projective geometry.

Also, welcome back! It has been a while since my last post. Hopefully I will find some time in the next couple of months to finish up the Modern OpenGL Series of articles. The code for article 08 is done, but writing the article will take some time.

Terminology

Most of the time when working with 3D, we are thinking in terms of Euclidean geometry – that is, coordinates in three-dimensional space (X$X$, Y$Y$, and Z$Z$). However, there are certain situations where it is useful to think in terms of projective geometry instead. Projective geometry has an extra dimension, called W$W$, in addition to the X$X$, Y$Y$, and Z$Z$ dimensions. This four-dimensional space is called "projective space," and coordinates in projective space are called "homogeneous coordinates."

For the purposes of 3D software, the terms "projective" and "homogeneous" are basically interchangeable with "4D."

Not Quaternions

Quaternions look a lot like homogeneous coordinates. Both are 4D vectors, commonly depicted as (X,Y,Z,W)$(X,Y,Z,W)$. However, quaternions and homogeneous coordinates are different concepts, with different uses.

The contents of this article don't apply to quaternions. If I can find the time, I might write a quaternion article in the future.

An Analogy In 2D

First, let's look at how projective geometry works in 2D, before we move on to 3D.

Imagine a projector that is projecting a 2D image onto a screen. It's easy to identify the X$X$ and Y$Y$ dimensions of the projected image:

The W$W$ dimension is the distance from the projector to the screen.

Now, if you step back from the 2D image and look at the projector and the screen, you can see the W$W$ dimension too. The W$W$ dimension is the distance from the projector to the screen.

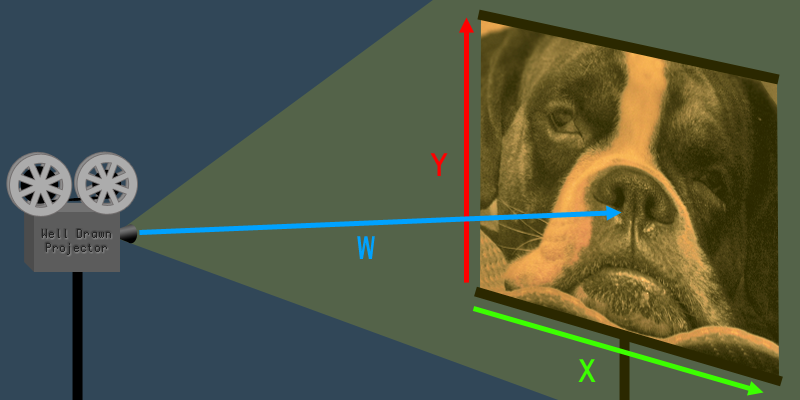
The value of W$W$ affects the size (a.k.a. scale) of the image.

So what does the W$W$ dimension do, exactly? Imagine what would happen to the 2D image if you increased or decreased W$W$ – that is, if you increased or decreased the distance between the projector and the screen. If you move the projector closer to the screen, the whole 2D image becomes smaller. If you move the projector away from the screen, the 2D image becomes larger. As you can see, the value of W$W$ affects the size (a.k.a. scale) of the image.

Applying It To 3D

There is no such thing as a 3D projector (yet), so it's harder to imagine projective geometry in 3D, but the W$W$ value works exactly the same as it does in 2D. When W$W$ increases, the coordinate expands (scales up). When W$W$ decreases, the coordinate shrinks (scales down). The W$W$ is basically a scaling transformation for the 3D coordinate.

When W = 1

The usual advice for 3D programming beginners is to always set W=1$W=1$ whenever converting a 3D coordinate to a 4D coordinate. The reason for this is that when you scale a coordinate by 1$1$ it doesn't shrink or grow, it just stays the same size. So, when W=1$W=1$ it has no effect on the X$X$, Y$Y$ or Z$Z$ values.

For this reason, when it comes to 3D computer graphics, coordinates are said to be "correct" only when W=1$W=1$. If you rendered coordinates with W>1$W>1$ then everything would look too small, and with W<1$W<1$ everything would look too big. If you tried to render with W=0$W=0$ your program would crash when it attempted to divide by zero. With W<0$W<0$ everything would flip upside-down and back-to-front.

Mathematically speaking, there is no such thing as an "incorrect" homogeneous coordinate. Using coordinates with W=1$W=1$ is just a useful convention for 3D computer graphics.

The Math

Now, let's look at some actual numbers, to see how the math works.

Let's say that the projector is 3$3$ meters away from the screen, and there is a dot on the 2D image at the coordinate (15,21)$(15,21)$. This gives us the projective coordinate vector (X,Y,W)=(15,21,3)$(X,Y,W)=(15,21,3)$.

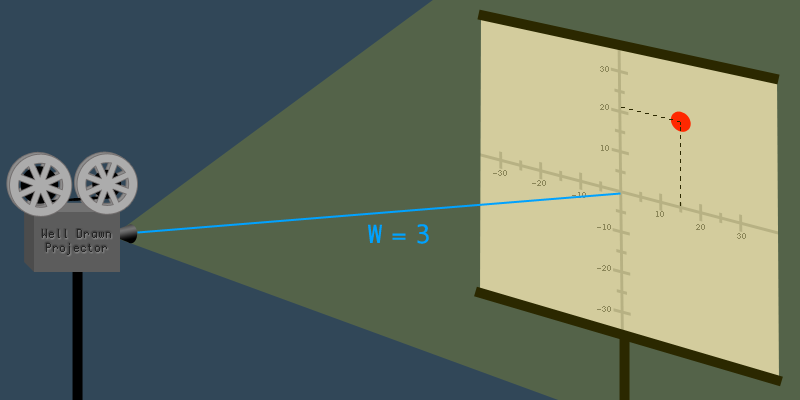
Now, imagine that the projector was pushed closer to the screen so that the distance was 1$1$ meter. The closer the project gets to the screen, the smaller the image becomes. The projector has moved three times closer, so the image becomes three times smaller. If we take the original coordinate vector and divide all the values by three, we get the new vector where W=1$W=1$:

(153,213,33)=(5,7,1)$$(\frac{15}{3},\frac{21}{3},\frac{3}{3})=(5,7,1)$$

The dot is now at coordinate (5,7)$(5,7)$.

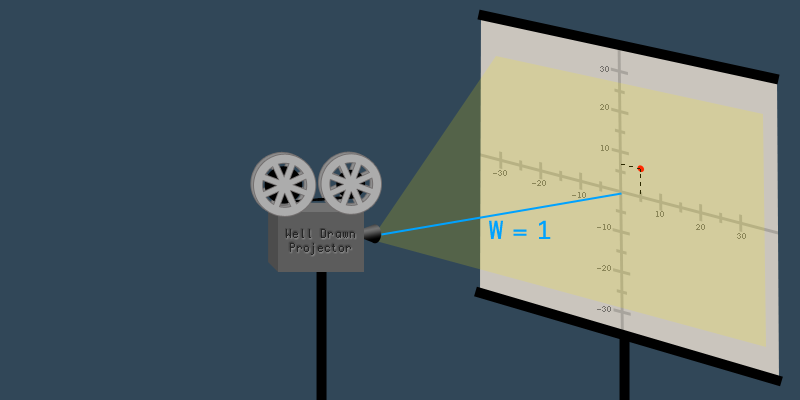
This is how an "incorrect" homogeneous coordinate is converted to a "correct" coordinate: divide all the values by W$W$. The process is exactly the same for 2D and 3D coordinates.

Dividing all the values in a vector is done by scalar multiplication with the reciprocal of the divisor. Here is a 4D example:

15(10,20,30,5)=(105,205,305,55)=(2,4,6,1)$$\frac{1}{5}(10,20,30,5)=(\frac{10}{5},\frac{20}{5},\frac{30}{5},\frac{5}{5})=(2,4,6,1)$$

Written in C++ using GLM, The example above would look like this:

glm::vec4 coordinate(10, 20, 30, 5);
glm::vec4 correctCoordinate = (1.0/coordinate.w) * coordinate;
//now, correctCoordinate == (2,4,6,1)